1.用在哪

1. hashmap (特指 Java 8 中的 HashMap)

 

• • 背景：在 Java 7 及之前，HashMap 处理哈希冲突（Hash Collision）的方法是使用链表。如果遭遇恶意攻击（Hash 碰撞攻击）或者哈希函数设计不佳，大量的 Key 会挤在同一个哈希桶里，导致链表极长。

• • 问题：链表的查询时间复杂度是 $O(N)$。如果链表长度达到 1000，查询效率直接退化成线性扫描，极其缓慢。

• • 红黑树的解法：从 Java 8 开始，当链表长度超过阈值（默认为 8）时，链表会自动转换为红黑树。

• • 优势：红黑树的查询复杂度是 $O(\log N)$。即使发生严重的哈希冲突，性能也不会崩盘，保证了最坏情况下的查询效率。

2. cfs (Linux Completely Fair Scheduler – 完全公平调度器)

 

• • 背景：操作系统需要决定“下一个让哪个进程使用 CPU”。CFS 的原则是：谁的 vruntime（虚拟运行时间）最小，谁就先运行（为了公平）。

• • 红黑树的作用：Linux 内核使用红黑树来组织所有处于“就绪状态”的进程任务。树的 Key 是进程的 vruntime。

• • 为什么用它？
    

     

    • • 红黑树是排序的，最左侧的叶子节点一定就是 vruntime 最小的任务。取出这个任务（调度执行）的速度非常快。
    • • 当进程运行了一段时间，vruntime 增加，需要把它重新插回树中；或者有新进程创建，也需要插入。红黑树的插入/删除操作（$O(\log N)$）足够快且性能稳定，适合内核这种高频调度的场景。

3. epoll (Linux 高性能 IO 多路复用)

 

• • 背景：在网络编程中，epoll 需要管理成千上万个 socket 连接（文件描述符 fd）。我们需要频繁地做三件事：添加监听(EPOLL_CTL_ADD)、删除监听(EPOLL_CTL_DEL)、修改监听事件(EPOLL_CTL_MOD)。

• • 红黑树的作用：在内核中，epoll 对象内部维护了一棵红黑树，用来存储所有被监听的 socket (fd)。

• • 为什么用它？
    

     

    • • 当你要添加一个 socket 时，内核需要快速检查它是否已经存在；
    • • 当你要删除一个 socket 时，内核需要快速找到它。
    • • 红黑树提供了稳定的查找和插入性能，即使面对百万级并发连接，增删改的时间复杂度依然稳定在 $O(\log N)$，不会像数组或链表那样随着连接数增加而性能骤降。

4. 定时器 (Timer)

 

• • 背景：服务器通常需要管理大量的定时任务（例如：30秒后断开连接、5秒后重发心跳）。系统需要快速找到“最近即将到期”的那个任务去执行。

• • 红黑树的作用：将所有的定时任务放入红黑树，Key 是“超时时间戳”。

• • 为什么用它？
    

     

    • • 红黑树是有序的，树中最左边的节点就是“最早会过期的任务”。
    • • 检查是否有任务超时只需要看最左节点，效率极高。
    • • 虽然也有用“时间轮（Timing Wheel）”或“最小堆（Min Heap）”实现的定时器，但红黑树在处理大量随机插入和删除定时任务时，表现非常均衡。

5. nginx如何用的 (Nginx 中的红黑树)

Nginx 是把红黑树用到极致的代表。它主要用在以下几个核心模块：

 

• • 定时器管理 (ngx_event_timer_rbtree)：正如上面第4点所述，Nginx 使用红黑树来管理所有的定时事件。它能快速找到最近过期的事件，也能快速删除被取消的定时器。

• • 文件缓存 / 目录树缓存：在处理静态文件请求时，Nginx 需要快速查找文件路径对应的缓存信息，这里也用到了红黑树进行索引。

• • Geo 模块：用于根据 IP 地址范围进行访问控制，利用红黑树的范围查找特性。

---

总结：为什么它们都选红黑树？

你看，无论是操作系统调度（CFS）、网络连接管理（epoll）、还是应用层服务器（Nginx），它们选择红黑树的理由惊人的一致：

 

1. 1. 有序：方便查找最小值（调度、定时器）或进行范围查找。

1. 1. 稳定：最坏情况下的时间复杂度也是 $O(\log N)$，不会像哈希表扩容那样出现由于数据量剧增导致的性能抖动（Jitter）。

1. 1. 读写均衡：相比于 AVL 树（追求极致平衡导致插入删除慢），红黑树在频繁插入删除（如进程切换、网络连接断开重连）的场景下，效率更高。

2. 强查找过程：

1. rbtree (红黑树 – Red-Black Tree)

 

• • 本质：一种自平衡的二叉查找树（BST）。

• • 查找复杂度：$O(\log n)$。

• • 核心特点：
    

     

    • • 通过旋转和变色保持树的近似平衡，防止退化成链表。
    • • 内存友好：主要用于内存中的有序数据存储。
    • • 相比 AVL 树，红黑树在插入/删除时的旋转次数更少，更适合写操作较多的场景。

• • 典型应用：
    

     

    • • C++ STL：std::map, std::set 的底层实现。
    • • Linux 内核：进程调度器（CFS）、Epoll 的内部管理。
    • • Java：HashMap 在冲突严重时（链表过长）会转化为红黑树。

2. hash (哈希表 – Hash Table)

 

• • 本质：通过哈希函数将 Key 映射到数组下标。

• • 查找复杂度：平均 $O(1)$，最坏 $O(n)$（发生大量碰撞时）。

• • 核心特点：
    

     

    • • 速度最快：点查询（Point Query）的王者。
    • • 无序性：数据是无序存储的，不支持范围查询（Range Query）。
    • • 需要处理哈希冲突（链地址法或开放寻址法）和扩容问题。

• • 典型应用：
    

     

    • • Redis：核心的 Key-Value 存储。
    • • 编程语言字典：Python dict, Go map, Java HashMap。
    • • 缓存系统：Memcached。

3. b/b+tree (B树 / B+树)

 

• • 本质：多路平衡查找树，专门为磁盘/存储系统设计。

• • 查找复杂度：$O(\log n)$，但树的高度极低。

• • 核心特点：
    

     

    • • 矮胖结构：一个节点包含多个 Key 和子节点，能极大减少磁盘 I/O 次数。
    • • B+树的优势：数据只存在于叶子节点，且叶子节点通过链表相连。这使得它非常适合范围查询（例如：SELECT * FROM users WHERE id > 100）。

• • 典型应用：
    

     

    • • 关系型数据库：MySQL (InnoDB 引擎), PostgreSQL, Oracle 的索引结构。
    • • 文件系统：NTFS, ext4 等文件系统的元数据管理。

4. 跳表 (Skip List)

 

• • 本质：一种基于链表的概率型数据结构，通过在链表上加“多级索引”来实现快速查找。

• • 查找复杂度：平均 $O(\log n)$。

• • 核心特点：
    

     

    • • 实现简单：相比红黑树复杂的旋转逻辑，跳表的代码实现要简单得多。
    • • 并发友好：在并发编程中，跳表的锁粒度更容易控制（通常只需局部锁），而红黑树调整平衡时往往涉及大范围变动。
    • • 支持有序存储和范围查询。

• • 典型应用：
    

     

    • • Redis：zset (Sorted Set) 的底层实现（用于排行榜等功能）。
    • • LevelDB / RocksDB：LSM-Tree 架构中的内存表（MemTable）通常使用跳表。

---

总结与对比 (Cheat Sheet)

特性	Hash (哈希表)	RBTree (红黑树)	B/B+ Tree	Skip List (跳表)
查找性能	$O(1)$ (最快)	$O(\log n)$	$O(\log n)$ (磁盘 I/O 少)	$O(\log n)$
是否有序	无序	有序	有序	有序
范围查询	不支持	支持 (中序遍历)	非常优秀 (B+树)	支持
主要场景	内存 KV 缓存	内存通用有序集合	磁盘数据库索引	高并发内存有序集合
代表应用	Redis, HashMap	C++ STL map, Linux	MySQL, Oracle	Redis ZSet, RocksDB

3. 红黑树的性质：

红黑树的 5 条性质 (CLRS 标准定义)

 

1. 1. 颜色属性：每个节点要么是红色，要么是黑色。

1. 1. 根属性：根节点必须是黑色。

1. 1. 叶子属性：所有的叶子节点（NIL 节点）*都是*黑色的。
      

       

      • • 注意：这里的叶子指的是为空的 NULL 指针，而不是存储数据的最后一层节点。

1. 1. 红色属性（不红红）：如果一个节点是红色的，则它的两个子节点必须是黑色的。
      

       

      • • 推论：一条路径上不能出现相邻的两个红色节点。

1. 1. 黑色属性（黑高一致）：对任意一个节点，从该节点到其所有后代叶子节点（NIL）的简单路径上，均包含相同数量的黑色节点。
      

       

      • • 这个数量被称为“黑高”（Black Height）。

---

为什么这 5 条性质能保证平衡？

这 5 条规则共同推导出了红黑树最关键的平衡推论：

从根到叶子的最长路径，不会超过最短路径的 2 倍。

 

• • 最短路径：全是黑色节点（根据性质5，黑色数量固定）。

• • 最长路径：红黑相间（根据性质4，红色不能相邻，所以最多是在每个黑色之间插一个红色）。

因此，红黑树虽然不是像 AVL 树那样的“绝对平衡”，但它是一种近似平衡。

总结记忆口诀

为了在面试中快速反应，可以记这个口诀：

 

1. 1. 非红即黑

1. 1. 头尾皆黑 （根是黑，NIL 叶子是黑）

1. 1. 红子必黑 （红节点的儿子一定是黑，也就是不能有两个连续红）

1. 1. 黑高相等 （任意路径上的黑节点数一样）

常见面试追问：

Q: 既然 AVL 树比红黑树更平衡，为什么 C++ STL (std::map) 和 Java (HashMap) 还要用红黑树？

 

• • AVL 树：结构非常严格，查找效率极高，但在插入/删除时，为了维护绝对平衡，需要频繁进行旋转操作，性能损耗大。

• • 红黑树：结构相对宽松（只要求最长路径不超过最短路径的2倍），插入/删除时旋转次数更少（插入最多旋转2次，删除最多旋转3次），在频繁写入的场景下性能更优。

树的高度最多为 2 * log(n+1)。

高效的查找、插入和删除（复杂度 O(log n)）

4. 红黑树的核心代码

1. 节点定义 (Node Structure)

红黑树比普通 BST 多了一个颜色位，且为了方便旋转，通常需要维护 parent 指针。

enum Color { RED, BLACK };

struct Node {
    int data;
    Color color;
    Node *left, *right, *parent;

    Node(int val) : data(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
    // 新插入节点默认为红色，因为插入红色破坏规则的可能性最小（只可能破坏性质4：不红红）
};

使用宏定义实现代码复用&&分离业务和数据

typedef int KEY_TYPE;

// 定义宏：用于生成包含左右子树、父节点和颜色的结构体
// 参数 name: 内部结构体的名称（如果传空则为匿名结构体）
// 参数 type: 指针指向的节点类型
#define RBTREE_ENTRY(name, type) \
    struct name {                \
        struct type *right;      \
        struct type *left;       \
        struct type *parent;     \
        unsigned char color;     \
    }

typedef struct _rbtree_node {

    KEY_TYPE key;
    void *value;

#if 0
    // 传统写法：直接在节点结构体中定义指针
    struct _rbtree_node *right;
    struct _rbtree_node *left;
    struct _rbtree_node *parent;
    unsigned char color;
#else
    // 宏封装写法：
    // 第一个参数为空，表示定义一个匿名结构体
    // 第二个参数 _rbtree_node，表示指针类型指向自身
    // 最终生成一个名为 node 的成员变量
    RBTREE_ENTRY(, _rbtree_node) node;
#endif

} rbtree_node;

thread场景

// 定义宏：用于生成包含左右子树、父节点和颜色的结构体
// 参数 name: 内部结构体的名称（如果传空则为匿名结构体）
// 参数 type: 指针指向的节点类型
#define RBTREE_ENTRY(name, type) \
    struct name {                \
        struct type *right;      \
        struct type *left;       \
        struct type *parent;     \
        unsigned char color;     \
    }

typedef struct thread {

    KEY_TYPE key;
    void *value;

#if 0
    // 传统写法：直接在节点结构体中定义指针
    struct _rbtree_node *right;
    struct _rbtree_node *left;
    struct _rbtree_node *parent;
    unsigned char color;
#else
    RBTREE_ENTRY(, thread) ready;  // 就绪状态的挂载点
    RBTREE_ENTRY(, thread) wait;   // 等待状态的挂载点
    RBTREE_ENTRY(, thread) sleep;  // 睡眠状态的挂载点
    RBTREE_ENTRY(, thread) exit;   // 退出状态的挂载点
#endif

} rbtree_node;

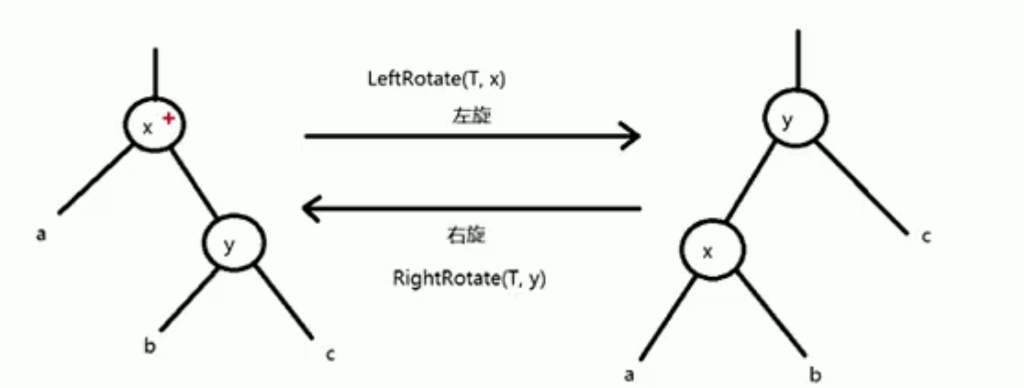
2. 左旋 (Left Rotate)

旋转是恢复平衡的基本操作。左旋和右旋是对称的，这里展示左旋。 核心逻辑：断开连接 -> 重新挂载 -> 更新父指针。

void leftRotate(Node* x) {
    Node* y = x->right; // y 是 x 的右孩子

 

 

   // 1. 把 y 的左孩子挂给 x 的右边
   x->right = y->left;
   if (y->left != nullptr) {
       y->left->parent = x;
  }

   // 2. 更新 y 的父节点
   y->parent = x->parent;
   if (x->parent == nullptr) {
       root = y; // x 原本是根
  } else if (x == x->parent->left) {
       x->parent->left = y;
  } else {
       x->parent->right = y;
  }

   // 3. 把 x 挂在 y 的左边
   y->left = x;
   x->parent = y;
}

3. 插入调整 (Insert Fixup) —— 最核心部分

这是面试最爱问的代码逻辑。当插入一个红色节点 z 后，如果父节点也是红色，就违反了“不红红”规则，需要分三种情况处理。

void insertFixup(Node* z) {
    // 只有当父节点存在且为红色时，才需要调整（违反性质4）
    while (z->parent != nullptr && z->parent->color == RED) {

 

 

       // — 场景 A：父节点是祖父的左孩子 —
       if (z->parent == z->parent->parent->left) {
           Node* uncle = z->parent->parent->right; // 叔叔节点

           // Case 1: 叔叔是红色
           // 策略：变色。父、叔变黑，祖父变红，当前节点上移到祖父。
           if (uncle != nullptr && uncle->color == RED) {
               z->parent->color = BLACK;
               uncle->color = BLACK;
               z->parent->parent->color = RED;
               z = z->parent->parent; // 指针上移，继续循环
          }
           else {
               // Case 2: 叔叔是黑色，且当前节点是右孩子 (折线/三角形)
               // 策略：先左旋变成 Case 3 (直线)
               if (z == z->parent->right) {
                   z = z->parent;
                   leftRotate(z);
              }

               // Case 3: 叔叔是黑色，且当前节点是左孩子 (直线)
               // 策略：父变黑，祖父变红，右旋祖父
               z->parent->color = BLACK;
               z->parent->parent->color = RED;
               rightRotate(z->parent->parent);
          }
      }
       // — 场景 B：父节点是祖父的右孩子 (与 A 完全对称) —
       else {
           Node* uncle = z->parent->parent->left;

 

           if (uncle != nullptr && uncle->color == RED) { // Case 1
               z->parent->color = BLACK;
               uncle->color = BLACK;
               z->parent->parent->color = RED;
               z = z->parent->parent;
          } else {
               if (z == z->parent->left) { // Case 2 (镜像)
                   z = z->parent;
                   rightRotate(z);
              }
               // Case 3 (镜像)
               z->parent->color = BLACK;
               z->parent->parent->color = RED;
               leftRotate(z->parent->parent);
          }
      }
  }
   // 最后时刻通过性质 2：根节点必须是黑色
   root->color = BLACK;
}

代码逻辑解析 (面试高频考点)

这段 insertFixup 处理了三种关键状态：

 

1. 1. Case 1 (红叔)：最简单。只需要重新着色。不仅解决了当前的冲突，还将“红色”向上推，可能导致上层冲突，所以需要 while 循环继续处理。

1. 1. Case 2 (黑叔 + 你的位置是内侧)：形成了“之”字形（Triangle）。需要先通过旋转把自己变成外侧节点（直线形），从而转化为 Case 3。

1. 1. Case 3 (黑叔 + 你的位置是外侧)：形成了“一”字形（Line）。通过一次旋转 + 变色彻底解决冲突，循环通常在此结束。

对情景A的解释

角色分配

为了方便理解，我们将涉及的节点命名如下：

 

• • z: 当前节点（新增节点，红色）。

• • Parent (P): 父亲节点（红色，且是 G 的左孩子）。

• • Grandparent (G): 祖父节点（黑色）。

• • Uncle (U): 叔叔节点（G 的右孩子）。

---

逻辑详细解析

1. 核心判断：看叔叔的颜色

代码的第一层逻辑是看叔叔 Uncle：

Node* uncle = z->parent->parent->right;

叔叔的颜色决定了我们要采取“简单策略”还是“复杂策略”。

2. Case 1: 叔叔是红色 (简单模式)

代码对应：

if (uncle != nullptr && uncle->color == RED) {
    z->parent->color = BLACK;       // 父亲变黑
    uncle->color = BLACK;           // 叔叔变黑
    z->parent->parent->color = RED; // 祖父变红
    z = z->parent->parent;          // 危机上移
}

 

• • 情景：父亲红，叔叔也红。

• • 策略：直接变色，不旋转。

• • 原理解释： 既然父亲和叔叔都是红的，那我就把他俩都涂黑，然后把那个黑色从祖父那里“借”过来（把祖父变成红）。 这样，经过父亲和叔叔路径的黑色节点数量（黑高）保持不变。

• • 后果：红色的冲突被推到了祖父那里。现在祖父变成了红色，但他自己的父亲可能也是红的，所以 z = z->parent->parent，把当前节点指向祖父，进入下一轮循环继续修。

---

3. Case 2: 叔叔是黑色 + 当前节点是右孩子 (折线/三角)

代码对应：

if (z == z->parent->right) {
    z = z->parent;
    leftRotate(z);
}

 

• • 情景：父亲红，叔叔黑（或者不存在/NIL）。且 z 是父亲的右孩子。

• • 形状：此时，祖父、父亲、z 形成了一个 < (小于号) 的折线形状（Left-Right）。

• • 策略：左旋父亲，把它拉直。

• • 原理解释： 折线形状很难直接通过一次旋转平衡。我们需要先把它变成一条直线（Case 3 的形状）。 这里对父亲进行左旋，z 就变成了父亲的父亲（结构上 z 上去了，原父亲下去了），但它们还是红红相邻。 注意：经过这一步，并没有解决红红冲突，只是为了把形状统一成 Case 3。

---

4. Case 3: 叔叔是黑色 + 当前节点是左孩子 (直线/一字)

代码对应：

z->parent->color = BLACK;           // 父亲变黑
z->parent->parent->color = RED;     // 祖父变红
rightRotate(z->parent->parent);     // 右旋祖父

 

• • 情景：父亲红，叔叔黑。且 z 是父亲的左孩子（如果是从 Case 2 掉下来的，此时的 z 指的是原来的父亲，已经在左边了）。

• • 形状：祖父、父亲、z 形成了一个 / (撇) 的直线形状（Left-Left）。

• • 策略：变色 + 右旋祖父。

• • 原理解释：
    

     

    1. 1. 变色：把父亲变黑（解决红红冲突），把祖父变红（保持黑高平衡）。
    1. 1. 旋转：这时候右边的黑高会少一个（因为祖父变红了），左边的黑高多了一个（因为父亲变黑了）。通过右旋祖父，把黑色的父亲提上去做根，红色的祖父降下来做右孩子。

• • 结果：平衡彻底恢复，红黑树性质满足，循环通常在此处终止。

---

图解总结

假设 G=祖父, P=父亲, U=叔叔, Z=当前节点。

Case 1 (叔叔红):

      G(黑)                 G(红)  <-- 问题上移
     /    \                /    \
   P(红)  U(红)   ==>    P(黑)  U(黑)
  /                     /
 Z(红)                 Z(红)

Case 2 (叔叔黑，折线):

      G(黑)                 G(黑)
     /    \                /    \
   P(红)  U(黑)   ==>    Z(红)  U(黑)  (变成 Case 3)
    \                    /
    Z(红)              P(红)

Case 3 (叔叔黑，直线):

      G(黑)                 P(黑)  <-- 平衡达成
     /    \                /    \
   P(红)  U(黑)   ==>    Z(红)   G(红)
  /                             \
 Z(红)                           U(黑)

一句话核心逻辑： “叔叔是红的就变色推锅；叔叔是黑的，如果是折线就先拉直，如果是直线就旋转解决。”